Таблица Брадиса является инструментом, который облегчает вычисления при решении различных задач, как в школьных предметах (математика, алгебра, геометрия и физика в старших классах), так и в университетах.
На нашем сайте представлены четырехзначные математические онлайн таблицы для тригонометрических функций, таких как синусы и косинусы. Кроме того, вы также найдете таблицы для тангенсов и котангенсов.
Как пользоваться таблицей Брадиса
В данном разделе мы проанализируем несколько примеров, чтобы понять, как эффективно использовать таблицу Брадиса.
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.
sin 3°42′ = 0.0645 (галочка выделена красным на изображении ниже) cos 80°24′ = 0.1668.
Имейте в виду, что аналогичные утверждения применимы и к вычислению значений тангенса и котангенса.
Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Важно помнить правило: для синуса корректировка имеет неотрицательный знак, а для косинуса — отрицательный.
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо
Таблица Брадиса: тангенсы, котангенсы, синусы и косинусы с инструкцией
Как бы не совершенствовалась вычислительная техника, определение синусов, косинусов, тангенсов и котангенсов с помощью таблицы Брадиса будет всегда актуально. Таблица Брадиса создана выдающимся педагогом-математиком Владимиром Модестовичем Брадисом. Чтобы вы научились пользоваться таблицами Брадиса, которые представлены ниже, рекомендуем сначала прочесть инструкцию.
Таблица брадиса — инструкция
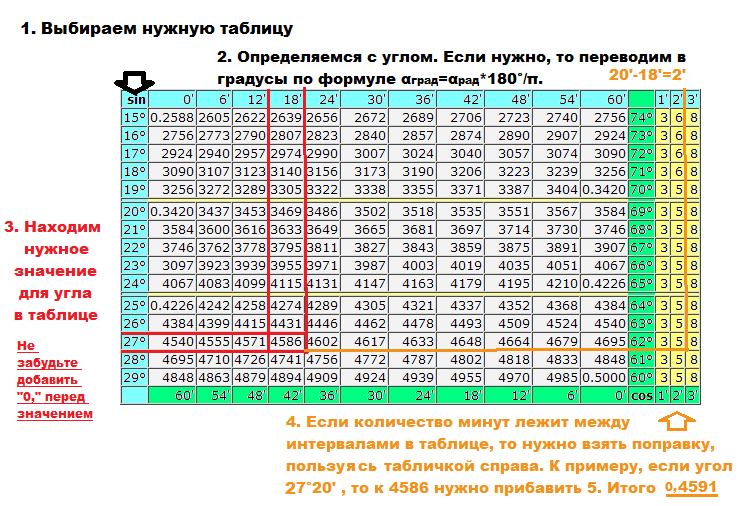
Таблица Брадиса: Косинусы-синусы
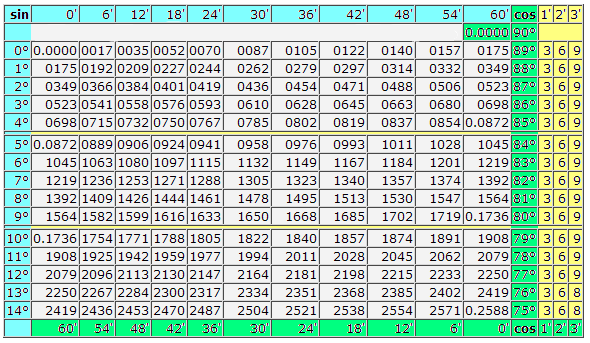
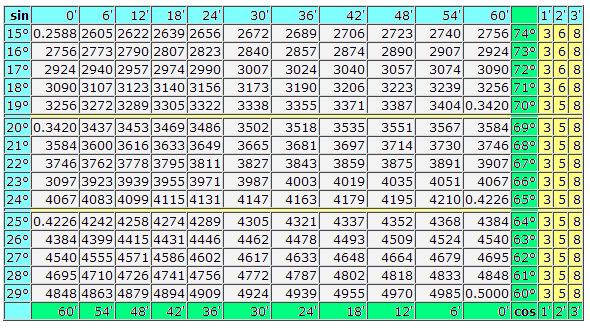
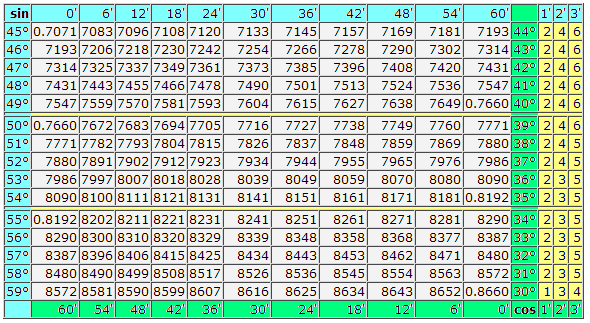
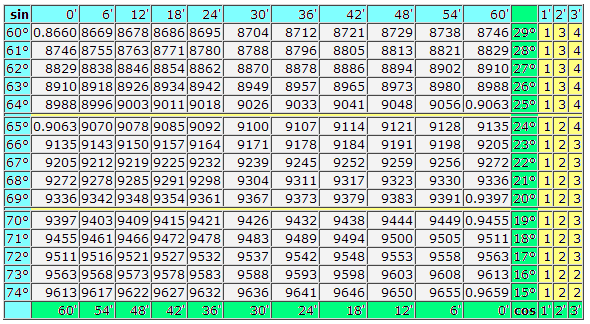
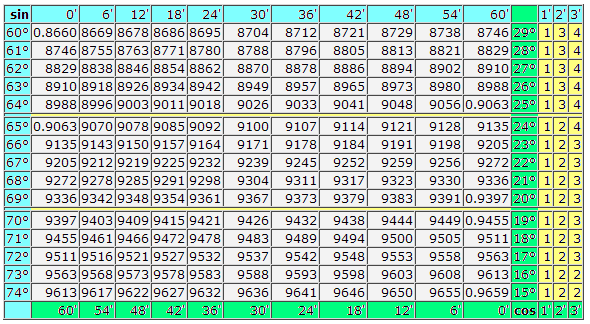
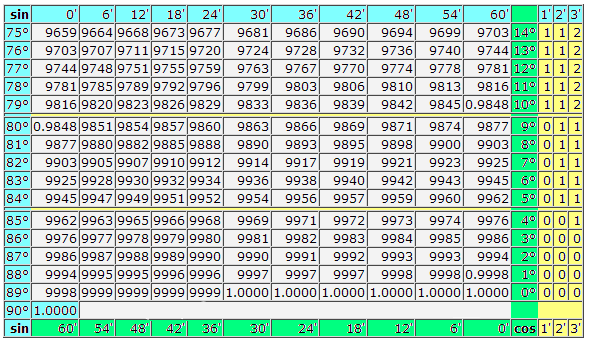
Таблица Брадиса: тангенсы — котангенсы
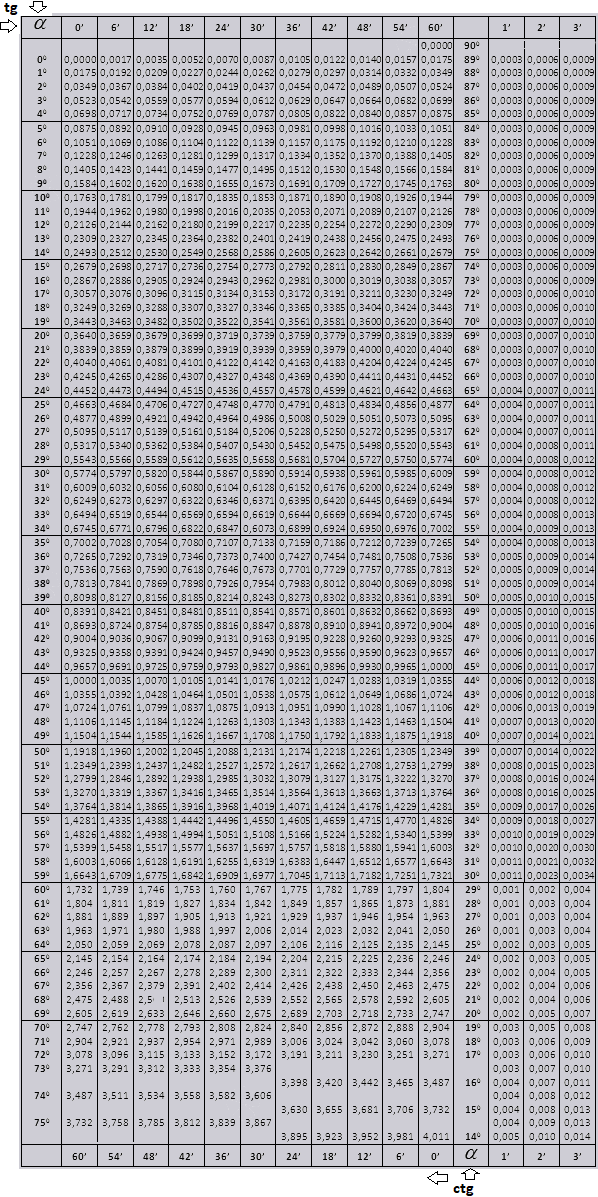
tg и ctg больших углов

tg и ctg малых углов
Если по пользованию таблицами Брадиса у вас возникли какие то вопросы, то пишите их в комментариях. Спасибо за пользование нашим сервисом.
Москвичей возможно заинтересует — дистанционное образование в москве. Учиться дистанционно — шикарная возможность стать свободнее уже сейчас.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
сб., 2015-08-15 16:47 — Marta
Просто случайно увидела эту статью. Назрел вопрос. В школе и в институте (моя сестра училась на бухгалтера и у них была высшая математика и мат.программирование) этой таблицей они не пользовались. Где же она тогда применяется, при обучении какой специальности ей пользуются?
четв., 2015-09-03 14:49 — Урсула
Я что то тоже не пойму где она используется, в смысле на каком факультете она преподается. Я училась на бухгалтера и у нас была высшая математика и мат.програмирование, но такой таблицы я не припомню.
ср., 2015-12-16 23:03 — Гость (не зарегистрирован)
Мы пользуемся этой таблицей школе (9 класс) на уроках геометрии , когда решаем треугольники (именно РЕШАЕМ треугольники ) по теоремам синусов и косинусов
сб., 2015-09-05 09:39 — Пифагоре
Не один день нужно практиковаться чтобы научится пользоваться этой замысловатой таблицей.
вс., 2015-09-06 21:35 — Saniya
Надеялся что никогда не придется этой таблицей воспользоваться, а все таки пришлось заглянуть сюда на сайт в ее поисках. спасибо автору, полная таблица в нашем распоряжении!
чт., 2017-12-28 04:46 — 11111111 (не зарегистрирован)
Здравствуйте, в Таблице Брадиса указан синус, а что делать, если нужен косинус
Таблица Брадиса. Синус, косинус
Независимо от уровня развития вычислительных технологий, использование таблицы Брадиса для нахождения значений синусов, косинусов, тангенсов и котангенсов останется всегда востребованным. Данная таблица была разработана выдающимся математиком и педагогом Владимиром Модестовичем Брадисом. Для того чтобы вы освоили работу с таблицами Брадиса, приведенными ниже, настоятельно рекомендуем сначала ознакомиться с инструкцией.
Таблица брадиса — инструкция
Вы уже знаете о суперспособностях современного учителя?
![]()
Тратить минимум сил на подготовку и проведение уроков.
![]()
Быстро и объективно проверять знания учащихся.
![]()
Сделать изучение нового материала максимально понятным.
![]()
Избавить себя от подбора заданий и их проверки после уроков.
![]()
Наладить дисциплину на своих уроках.
![]()
Получить возможность работать творчески.