В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20.
Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа. Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
- Последовательно выполнять деление десятичного числа и получаемых целых частных на 2, до тех пор, пока частное не станет равным 0.
- Для получения ответа в двоичном коде, необходимо записать, полученные, в результате деления остатки, в обратном порядке.
Пример 1 : перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
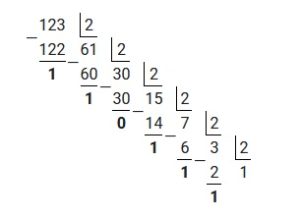
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в двоичную систему
- Последовательно выполнять умножение исходной дроби на 2, до тех пор, пока, дробная часть не станет равна 0 или пока не будет достигнута необходимая точность вычисления.
- Полученная дробь в двоичной системе будет равна прямой последовательности целых частей произведений.
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0) 0.246 ∙ 2 = 0.492 (0) 0.492 ∙ 2 = 0.984 (0) 0.984 ∙ 2 = 1.968 (1) 0.968 ∙ 2 = 1.936 (1) 0.936 ∙ 2 = 1.872 (1) 0.872 ∙ 2 = 1.744 (1) 0.744 ∙ 2 = 1.488 (1) 0.488 ∙ 2 = 0.976 (0) 0.976 ∙ 2 = 1.952 (1) 0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
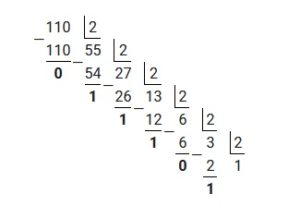
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1) 0.25 ∙ 2 = 0.5 (0) 0.5 ∙ 2 = 1 (1)
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Задача: перевести число 37.14 из десятичной системы счисления в двоичную.
Для того, чтобы перевести число 37.14 из десятичной системы счисления в двоичную, необходимо перевести вначале целую часть, а затем дробную. Таким образом потребуется:
- Перевести 37 в двоичную систему;
- Перевести 0.14 в двоичную систему.
1. Для того, чтобы перевести число 37 из десятичной системы счисления в двоичную, необходимо осуществить последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.
| — | 37 | 2 | ||
| 36 | — | 18 | 2 | |
| 1 | 18 | — | 9 | 2 |
| 0 | 8 | — | 4 | 2 |
| 1 | 4 | — | 2 | 2 |
| 0 | 2 | 1 | ||
| 0 |
Полученные остатки записываем в обратном порядке, таким образом:
2. Для перевода десятичной дроби 0.14 в двоичную систему, необходимо выполнить последовательное умножение дроби на 2, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. Получаем:
0.14 ∙ 2 = 0.28 (0) 0.28 ∙ 2 = 0.56 (0) 0.56 ∙ 2 = 1.12 (1) 0.12 ∙ 2 = 0.24 (0) 0.24 ∙ 2 = 0.48 (0) 0.48 ∙ 2 = 0.96 (0) 0.96 ∙ 2 = 1.92 (1) 0.92 ∙ 2 = 1.84 (1) 0.84 ∙ 2 = 1.68 (1) 0.68 ∙ 2 = 1.36 (1) 0.36 ∙ 2 = 0.72 (0)
Ответом станет прямая последовательность целых частей произведения. Т.е.
3. Осталось соединить переведенные части, таким образом:
Подробнее о том, как переводить числа из десятичной системы в двоичную, смотрите здесь.
Пример 4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа 22 оканчивается на 4.
Поскольку запись числа в системе счисления с основанием q заканчивается на 4, остаток от деления числа 22 на q равен 4: 22 mod q = 4 1) . Следовательно, 18 mod q = 0. Это верно для q ? .
1) Операция mod — вычисление остатка от целочисленного деления.
Так как в новой системе счисления запись числа оканчивается на 4, то q > 4. Следовательно, условию задачи удовлетворяют основания: 18, 9 и 6.
Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16. 512=2 9 . 51210=1 000000000 2. 16=2 4 . 1610=1 0000 2. Теперь сложим столбиком:
В компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют компьютерными. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!

7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Перевод чисел из одной системы счисления в другую
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
Чтобы быстро переводить числа из десятичной системы счисления в двоичную, нужно хорошо знать числа «2 в степени». Например, 2 10 =1024 и т.д. Это позволит решать некоторые примеры на перевод буквально за секунды. Одной из таких задач является задача A1 из демо ЕГЭ 2012 года. Можно, конечно, долго и нудно делить число на «2».
Но лучше решать по-другому, экономя драгоценное время на экзамене.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Если число, которое нужно перевести, меньше числа «2 в степени» на 1, то в двоичной системе это число состоит только из единиц, количество которых равно степени.
- Переведем 3 из десятичной системы. 3=2 2 -1. Поэтому в двоичной системе число содержит 2 единицы . Получаем 11 2.
- Переведем 7 из десятичной системы. 7=2 3 -1. Поэтому в двоичной системе число содержит 3 единицы . Получаем 111 2.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Аналогичен перевод и для других чисел «2 в степени-1».
Понятно, что перевод чисел от 0 до 8 можно сделать быстро или делением, или просто знать наизусть их представление в двоичной системе. Я привела эти примеры, чтобы Вы поняли принцип данного метода и использовали его для перевода более «внушительных чисел», например, для перевода чисел 127,128, 255, 256, 511, 512 и т.д.
Можно встретить такие задачи, когда нужно перевести число, не равное числу «2 в степени», но близкое к нему. Оно может быть больше или меньше числа «2 в степени». Разница между переводимым числом и числом «2 в степени» должна быть небольшая. Например, до 3. Представление чисел от 0 до 3 в двоичной системе надо просто знать без перевода.
Переводим сначала число «2 в степени» в двоичную систему. А потом прибавляем к нему разницу между числом «2 в степени» и переводимым числом.
Например, переведем 19 из десятичной системы. Оно больше числа «2 в степени» на 3.
Если число меньше числа «2 в степени», то удобнее пользоваться числом «2 в степени-1». Решаем так:
Переводим сначала число «2 в степени-1» в двоичную систему. А потом вычитаем из него разницу между числом «2 в степени-1» и переводимым числом.
Например, переведем 29 из десятичной системы. Оно больше числа «2 в степени-1» на 2. 29=31-2.
Если разница между переводимым числом и числом «2 в степени» больше трех , то можно разбить число на составляющие, перевести каждую часть в двоичную систему и сложить.
Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16. 512=2 9 . 51210=1 000000000 2. 16=2 4 . 1610=1 0000 2. Теперь сложим столбиком:
Данная методика позволяет тратить минимум времени на перевод чисел из десятичной системы в двоичную, но при условии, что Вы прекрасно знаете числа «2 в степени». Если это не так, то заучите эти числа. Тем более, что в задачах по информатике они активно используются.
Число в двоичной системе представить как последовательность последнего результата деления и остатков от деления в обратном порядке. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
3.3. Правила перевода чисел из одной системы счисления в другую
1. Перевести число 1001101.11012 в десятичную систему счисления. Решение: 1001101.11012 = 1·2 6 +0·2 5 +0·2 4 +1·2 3 +1·2 2 +0·2 1 +1·2 0 +1·2 -1 +1·2 -2 +0·2 -3 +1·2 -4 = 64+8++4+1+0.5+0.25+0.0625 = 77.812510 Ответ: 1001101.11012 = 77.812510
Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.
1. Перевод смешанного числа в десятичную систему счисления из любой другой.
Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Переведите число 105,4 из восьмеричной системы в десятичную.
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :

Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
2. Перевод десятичных дробей из десятичной системы счисления в любую другую.
Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.
Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:

Переведите десятичное число 0,8125 в восьмеричную систему.
Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:

3. Перевод смешанных чисел из десятичной системы счисления в любую другую
Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.
- Smart things что это за программа на андроид
- Как удалить вайбер с планшета полностью
- Как скопировать высоту строк в excel
- Outlook express код ошибки 0x800ccc18
- Как сделать кожу золотистой фотошоп
Как вставлять римские цифры в Microsoft Word
При оформлении документов Microsoft Word иногда приходится использовать вместо традиционных арабских цифр римские. Если речь идет о создании нумерованных списков, то здесь нет никаких проблем, просто жмем «Нумерация» в блоке «Абзац», выбираем римский формат и тут же получаем результат. Иное дело, когда римскую цифру нужно вставить где-то в предложении.
Ни в приложениях Microsoft Office, ни тем более на клавиатуре нет переключателя, который позволил бы автоматически конвертировать арабские цифры в римские.
Пользоваться кодами ASCII — настоящая головная боль, использовать латиницу — нужно знать римский счет, а многие умеют считать до десяти или максимум до сорока.
Вот как, например, записать римскими цифрами 2522?
Нужно вспомнить, что 1000 по-римски это M, а 500 — это D, ну а дальше, вроде, всё понятно: 10 — это X, значит 22 будет XXII. Если же погружаться в историю желания нет, вот два способа решить проблему.
Онлайн-конвертеры
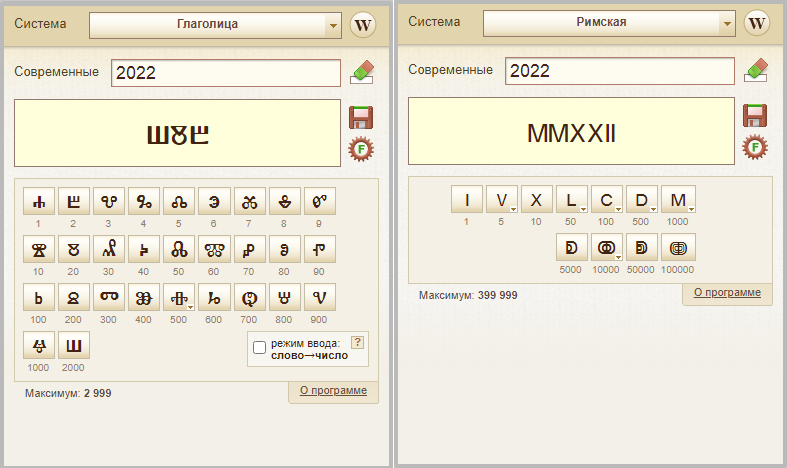
В сети существует множество конвертеров, позволяющих преобразовывать различные системы счисления, в том числе конвертировать современные арабские цифры не только в римские, но и в греческие, персидские, кхмерские, тайские, тибетские и даже в старославянские.
В качестве примера такого специального онлайн-конвертера можно привести numbers.alter-world.net, поддерживающего работу с позиционными и непозиционными буквенными системами счисления. Но это уже экзотика, в отличие от римских, использовать записанные глаголицей цифры вам вряд ли придется.
Формула Word
Можно обойтись и без сторонних конвертеров, потому что преобразовывать арабские цифры в римские умеет и сам Word.
Чтобы вставить в текст римскую цифру, сделайте следующее:
- Нажмите на клавиатуре Ctrl + F9 ;
- В появившихся затемненных фигурных скобках вставьте знак равенства, затем введите преобразуемое число;
- За числом вставьте слеш, звездочку и напишите ROMAN или roman в зависимости от того, нужна ли вам большая или маленькая римская цифра. Вот так: ;
- Нажмите F9 , чтобы применить формулу.

К сожалению, используемая в Word формула мало подходит для преобразования больших чисел.
Так, 10000 она запишет как MMMMMMMMMM, тогда как согласно правилам римского счисления, цифры I, X, C и M не могут повторяться более трех раз подряд. Для записи больших чисел следует использовать либо специальные символы, либо верхнее подчеркивание, увеличивающее значение цифры в 1000 раз.
Римские цифры в Ворде
Обычно мы пользуемся арабскими цифрами, но при нумерации научных статей или написании исторических текстов порой приходится возвращаться к символам, которые использовали еще древние римляне. Написать римские цифры в Ворде реально, даже несмотря на то, что на клавиатуре нужных знаков нет. Однако есть целых три способа устранения этого недостатка.
Использование английской раскладки
Самый простой и часто используемый способ написать римские цифры в документе Word – переключить раскладку на клавиатуре и составить нужные значения из латинских букв.

- Измените раскладку (Ctrl+Shift или Alt+Shift).
- Включите Caps Lock, чтобы вводимые буквы были заглавными.
- Составьте нужное число из латинских букв.
Минус этого способа в том, что для его применения требуется знание римской системы счисления. В принципе, это не так сложно, но большинство пользователей знает, как пишутся только простые числа. Если счет идет на сотни или тысячи, неизбежно возникнут трудности
Конвертация через формулу
Чтобы не запоминать, как пишутся большие числа римскими цифрами, и не вводить значения вручную латинскими буквами, воспользуйтесь специальной формулой. Да, в Word тоже есть формулы: не такие функциональные, как в Excel, но чрезвычайно полезные.

- Поставьте курсор на место, куда нужно вписать цифровые данные. Нажмите сочетание Ctrl+F9.
- На месте курсора появятся закругленные скобки. Вставьте в них формулу =число/*Roman и нажмите F9.
Не забывайте делать пробелы – должно получиться вот так < =541*Roman >. Если пробелов между скобками и формулой не будет, то Word покажет наличие синтаксической ошибки.
Выбор формата нумерации
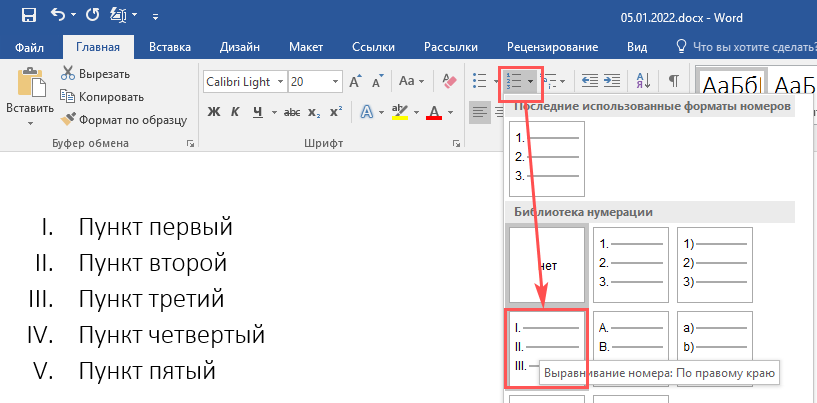
Если римские цифры нужны для использования в нумерованном списке, то перечисленные выше способы не подойдут. Благо, среди функций Word есть изменение формата нумерации. Познакомимся с ним поближе:

- Введите первый пункт перечисления.
- Найдите на вкладке «Главная» раздел «Абзац».
- Раскройте библиотеку нумераций.
- Выберите вариант с использованием римской системы счисления.
Возле первой строчки списка появится цифра «i». При нажатии клавиши Enter и вводе последующих пунктов перечисления нумерация будет автоматически продолжаться – i, ii, iii, iv и так далее, пока не закончится список.
Похожие статьи:
- Способы нумерации страниц в Word