Как создать таблицу интегралов в Word

Таблица интегралов

Для быстрого интегрального исчисления нужно знать, как искать производные простой и сложной функции. Ведь нахождение интеграла и производных являются взаимно обратные операции. Для интегрирования потребуются: таблица интегралов полная и также формулы интегралов таблица основных свойств, таблица производных и интегралов.

У многих возникает сложность в изучении и понимании неопределенных интегралов. Если производные обладают всего лишь 5 правилами дифференцирования, четким алгоритм, таблицей производных, то при интегрировании совсем иначе. Используются десятки приемов и способов интегрирования. При неверном выборе способа интегрирования и различного метода интеграл вычислять можно долго, так как он представляет собой некий ребус.

Определение первообразной

Определение

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство (F(x)+C)׳=f(x). Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла

Определение

Совокупность функций первообразной для данной функции y=f(x), которая имеет место на некотором отрезке [a;b], называют неопределенным интегралом y=f(x).

Неопределенный интеграл имеет обозначение: [int f(x) d x=F(x)+C, c=text < const >].

Определение интегрирования

Определение

Операция нахождения интеграла называется интегрированием.

Дифференциал с интегральным выражением являются взаимно обратными действиями. У любой непрерывной на интервале функции есть какой-либо неопределенный интеграл.

Кратко о терминах и обозначениях:

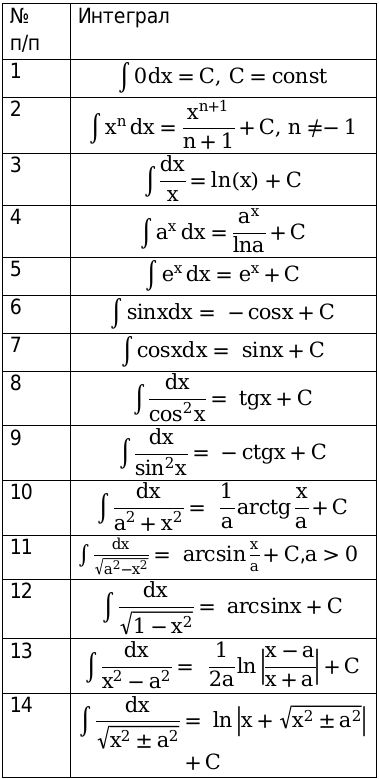
Таблица производных не включает формулы, которые соответствуют формулам из 10,13,14 таблицы. Чтобы проверить справедливость формул, необходимо произвести дифференцирование над ними.

Формулы интегралов, полная таблица основных свойств:

Расшифровка свойств интегралов:

1. Неопределенный интеграл при интегрировании функции является равным предоставляемой функции.
2. Производная от интегрального выражения будет равна подынтегральной функции, а дифференциал будет равен подынтегральному выражению.
3. Множитель в виде числа можно выносить за интеграл.
4. Интегральное выражение от суммы функций имеет такое же значение, как сумма интегральных выражений.
5. Подынтегральное выражение с множителями внутри равен подынтегральному выражению с выносимой константой.

C помощью них можно упростить выражение интеграла и вычислить элементарными действиями.

Стоит рассмотреть примеры для лучшего восприятия темы:

Вычислить интеграл и сделать проверку:

[intleft(x+sqrt-3 x^+frac>-frac <sin ^x>+t g 5right) d x]

Вычислим интеграл, раскрывая скобки. При этом знак интеграла относится к каждому члену выражения.

Берем в использование свойство интеграла в этом же действии:

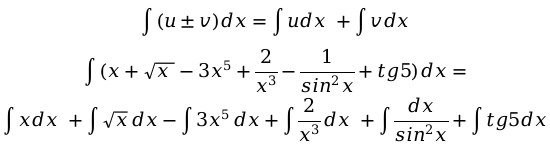
Вынесем все существуемые константы за знак интеграла — в данном случае они представляют собой числа. Стоит обратить внимание, что последнее выражение tg5 — это и является константа, её Выносим.

На этом этапе стоит преобразовать степени, корни для интегрирования. Как при дифференцировании, корни представляем в формате [x^>]. Степени и корни, которые стоят в знаменателе переносим наверх с противоположным знаком.

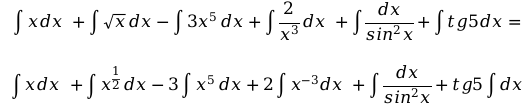
Используя таблицу основных интегралов, интегрируем:

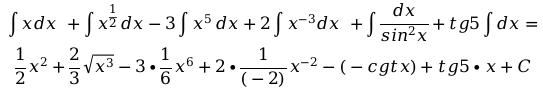
И окончательный ответ:

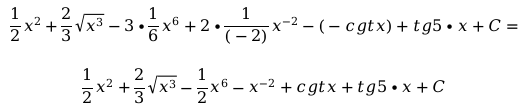
Примечание: В этом примере содержатся и используются только табличные интегралы. Все превращения осуществляются с помощью данных формул:

[ int frac x>=-operatorname x+C, int x^ d x=frac>+C, n neq-1, int d x=x+C ]

Стоит обратить внимание на формулу степенной функции: [int x^ d x=frac>+C, n neq-1], которая встречается почти в каждом примере.

Интеграл [int d x=x+C] является частным случаем табличного интеграла: [int d x=int x^ d x=frac cdot x^+C=x+C].

Константу C ставится только один раз в конечном выражении. Ставить после каждого интеграла не стоит.

Выполним проверку. Для выполнения проверки необходимо продифференцировать найденное выражение, то есть найти производную:

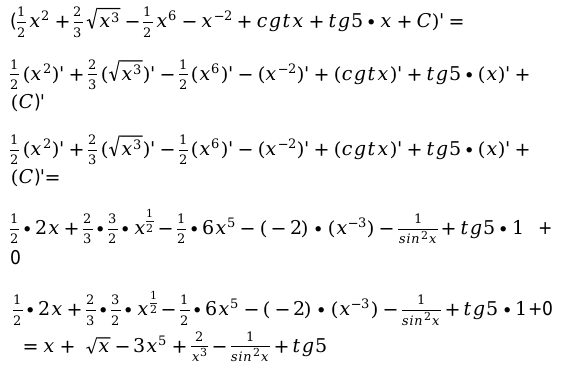
Если получилось исходное выражение, то интеграл был вычислен верно.

Раскрытие дифференциала происходит так:

1. знак d необходимо убрать;
2. ставится штрих справа над скобкой, чтобы обозначить производную;
3. в конечное выражение добавляется множитель dx

Например: [d(2 x-1)=(2 x-1)^ <prime>d x=(2-0) d x=2 d x]

Проверить правильность табличного интеграла:

[int operatorname x d x=ln |sin x|+C, C=mathrm t]

Найдем производную от правой части выражения:

[ ln |sin x|+C(ln |sin x|)^<prime>=frac cdot cos x=operatorname x ]

Производная получилось такая же, как и подынтегральная функция. Поэтому формула является верной.

Вычислить интеграл:

[ int(cos (3 x+2)+5 x) d x ]

Используем одно из основных свойств:

[ int(cos (3 x+2)+5 x) d x=int(cos (3 x+2)) d x+int 5 x d x ]

Используем свойство о вынесении множителя за интеграл:

[ int(cos (3 x+2)) d x+int 5 x d x=int(cos (3 x+2)) d x+5 int x d x ]

С помощью таблицы:

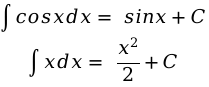
При вычислении воспользуемся 5 свойством:

[ int(cos (3 x+2)) d x=frac<1> sin (3 x+2)+C_ <1>]

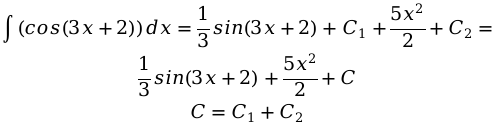
При этом C1+C2 являются частями C. Если отдельно решается 2 и более интегралов, то к каждому члену ставится C с определенным индексом.

Нет времени решать самому?

Решение интегралов. Рассказываем, как решать интегралы

Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы! Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.

Решение интегралов (интегрирование) есть операция обратная дифференцированию. Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены.

Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему. В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b . Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b. Не верится?

Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим: Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.

Попробуем решить тоже самое не прибегая к построению, используя интегрирование: Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.

Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной. F(x) – первообразная. Дифференцируя первообразную, мы получим исходное подынтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференцируем полученный ответ и сравниваем с исходным выражением. Основные функции и первообразные для них приведены в таблице:

Таблица первообразных для решения интегралов

Основные приемы решения интегралов: Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду. Сначала следует запомнить основные свойства интегралов:

Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.

Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.

Основные приемы решения интегралов

1. Замена переменной. Для выполнения данного приема потребуется хороший навык нахождения производных.

2. Интегрирование по частям. Пользуются следующей формулой. Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.

3. Интегрирование дробно-рациональных функций. — разложить дробь на простейшие — выделить полный квадрат. — создать в числителе дифференциал знаменателя.

4. Интегрирование дробно-иррациональных функций. — выделить под корнем полный квадрат — создать в числителе дифференциал подкоренного выражения. 5. Интегрирование тригонометрических функций. При интегрировании выражений вида применяет формулы разложения для произведения. Для выражений m-нечетное, n –любое, создаем d(cosx). Используем тождество sin 2 +cos 2 =1 m,n – четные, sin 2 x=(1-cos2x)/2 и cos 2 x=(1+cos2x)/2 Для выражений вида: — Применяем свойство tg 2 x=1/cos 2 x — 1

С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм: Алгоритм обучения решению интегралов:

1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования.

Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию. 2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных.

По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен. 3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения.

В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя. Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференцируем полученное выражение и сравниваем с исходным интегралом. Отработаем основные моменты на нескольких примерах:

Примеры решения интегралов

Пример 1: Решить интеграл: 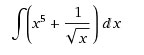Интеграл неопределенный. Находим первообразную. Для этого интеграл суммы разложим на сумму интегралов. 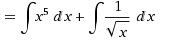Каждый из интегралов табличного вида. Смотрим первообразные по таблице. Решение интеграла: 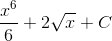Проверим решение(найдем производную):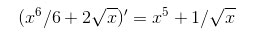

Пример 2. Решаем интеграл

Интеграл неопределенный. Находим первообразную. Сравниваем с таблицей. В таблице нет. Разложить, пользуясь свойствами, нельзя.

Смотрим приемы. Наиболее подходит замена переменной. Заменяем х+5 на t 5 . t 5 = x+5 . Получаем.

Но dx нужно тоже заменить на t. x= t 5 — 5, dx = (t 5 — 5)’ = 5t 4 . Подставляем:

Интеграл из таблицы. Считаем:

Подставляем в ответ вместо t ,

Пример 3. Решение интеграла: 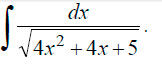Для решения в этом случае необходимо выделить полный квадрат. Выделяем: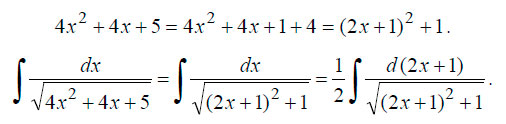

В данном случае коэффициент 1/2 перед интегралом получился в результате замены dx на 1/2*d(2x+1). Если вы найдете производные x’ = 1 и 1/2*(2x+1)’= 1, то поймете почему так. В результате мы привели интеграл к табличному виду. Находим первообразную. 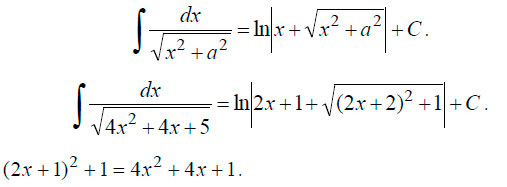В итоге получаем: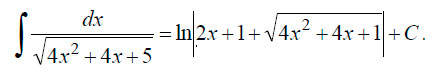

Для закрепления темы интегралов рекомендуем также посмотреть видео. В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.

Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.

Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию . Программирование одна из дочек математики!

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

• Блог пользователя admin
• Войдите на сайт для отправки комментариев