Если вам необходимо написать вектор в Microsoft Word, есть несколько способов сделать это. В данной статье мы рассмотрим два основных метода: с использованием уравнения и с использованием символов.
В следующих разделах мы подробнее рассмотрим каждый способ и предоставим пошаговую инструкцию о том, как написать вектор с помощью каждого из них. Вы также узнаете о некоторых дополнительных функциях Word, которые помогут вам создавать и редактировать векторы с легкостью. Продолжайте чтение, чтобы узнать, как правильно написать вектор в ворде и сделать ваш документ более профессиональным и наглядным.

Определение вектора
В физике и математике вектор – это математический объект, который характеризуется направлением и величиной. Он служит для описания физических величин, которые имеют не только величину, но и определенное направление. Вектор может быть представлен как стрелка, у которой есть начало и конец. Начало стрелки соответствует начальной точке, а конец – конечной.
Векторы широко используются во многих областях науки и техники, включая физику, инженерию, компьютерную графику и многие другие. Векторы могут представлять различные физические величины, такие как сила, скорость, ускорение и многие другие.
Основные характеристики вектора
Вектор характеризуется следующими основными характеристиками:
- Направление: вектор указывает на определенное направление в пространстве. Направление может быть задано с помощью угла между вектором и определенной осью или другим вектором.
- Величина: вектор имеет определенную величину или длину, которая может быть измерена в соответствующих единицах измерения. Например, вектор скорости может иметь длину 50 метров в секунду.
- Начало и конец: вектор имеет начальную и конечную точку, которые определяют его положение в пространстве. Начало вектора обычно обозначается точкой O, а конец – точкой A.
Графическое представление вектора
Вектор может быть представлен графически с помощью стрелки, у которой начало находится в точке O, а конец – в точке A. Направление стрелки указывает на направление вектора, а длина стрелки – на его величину. Если два вектора равны по направлению и величине, то они называются равными.
| Обозначение | Описание |
|---|---|
| AB | Вектор, соединяющий начальную точку O и конечную точку A. |
| |AB| | Длина вектора AB. |
Таким образом, вектор – это математический объект, который позволяет описывать физические величины с направлением и величиной. Использование векторов позволяет более точно и наглядно описывать и анализировать различные явления и процессы в природе и технике.
MS Word Векторная графика
Что такое вектор?
Вектор – это фундаментальное понятие в математике и физике, которое используется для описания и измерения направления и величины физических величин. Он представляет собой математический объект, который имеет как направление, так и длину.
Вектор может быть представлен как упорядоченный набор чисел, называемых компонентами вектора, или как стрелка, указывающая на определенную точку в пространстве. Компоненты вектора могут быть числами или переменными, которые представляют физические величины, такие как скорость, сила или положение.
Основные характеристики вектора:
- Направление: вектор указывает на определенное направление в пространстве. Направление может быть определено в виде угла с осью координат или как отношение компонент вектора.
- Длина или модуль: вектор имеет определенную длину, которая может быть измерена или рассчитана с использованием определенных математических формул.
- Сложение и вычитание: векторы могут быть сложены или вычтены друг из друга для получения нового вектора, который представляет собой сумму или разницу исходных векторов.
- Умножение на скаляр: векторы могут быть умножены на скалярное число, что приведет к изменению их длины, но не направления.
- Скалярное произведение: векторы могут быть перемножены с использованием скалярного произведения для получения скалярной величины, которая может быть использована для определения угла между векторами или проекции одного вектора на другой.
- Векторное произведение: векторы могут быть перемножены с использованием векторного произведения для получения нового вектора, перпендикулярного исходным векторам.
Векторы играют важную роль в различных областях, включая физику, геометрию, инженерию и компьютерную графику. Они используются для моделирования и анализа различных физических явлений, решения задач, определения направления движения и многих других приложений.

Свойства вектора
1. Направление и длина:
Вектор характеризуется своим направлением и длиной. Направление вектора указывает на то, куда он направлен в пространстве, а длина – на его размер. Направление может быть задано углом между вектором и определенной осью или плоскостью, а длина – числовым значением, которое обозначает, насколько далеко вектор простирается.
2. Сложение:
Векторы можно складывать, при этом получается новый вектор, который называется суммой и обозначается символом «+». При сложении векторов их направления и длины учитываются. Сложение векторов выполняется путем соединения начал векторов и проведения прямой, которая соединяет концы. Полученная прямая является суммой векторов.
3. Вычитание:
Векторы можно также вычитать, получая новый вектор, называемый разностью и обозначаемый символом «-«. Вычитание вектора аналогично сложению, но вместо соединения прямыми начал и концов векторов проводится прямая, которая проходит через конец первого вектора и начало второго вектора. Полученная прямая является разностью векторов.
4. Умножение на число:
Векторы можно умножать на число, получая новый вектор, который называется произведением вектора на число и обозначается символом «·». При умножении вектора на число его направление сохраняется, а длина изменяется. Если число положительное, то длина вектора увеличивается в соответствии с этим числом, если число отрицательное, то длина вектора уменьшается с сохранением направления.
5. Скалярное произведение:
Скалярное произведение двух векторов определяет числовую величину и равно произведению длин векторов на косинус угла между ними. Скалярное произведение векторов обозначается символом «·» или «скалярным умножением«. Результат скалярного произведения векторов является числом.
6. Векторное произведение:
Векторное произведение двух векторов определяет вектор, перпендикулярный плоскости, в которой лежат данные векторы. Векторное произведение векторов обозначается символом «x» или «векторным умножением«. Кроме того, векторное произведение обладает свойством антикоммутативности, то есть изменение порядка векторов в произведении меняет его направление на противоположное.
7. Единичный вектор:
Единичный вектор – это вектор, длина которого равна 1. Умножение вектора на число называется масштабированием вектора, и если число имеет длину 1, то масштабирование приводит к получению единичного вектора, указывающего в том же направлении, что и исходный вектор.
8. Коммутативность и ассоциативность:
Сложение и умножение векторов обладают свойствами коммутативности (изменение порядка векторов не меняет результата) и ассоциативности (порядок выполнения операций не влияет на результат).

Способы создания вектора в Microsoft Word
Microsoft Word является одним из самых популярных текстовых редакторов, который также предоставляет инструменты для создания векторных изображений. Векторная графика отличается от растровой тем, что она состоит из математических объектов, таких как линии, кривые и фигуры, а не из пикселей. В данной статье мы рассмотрим несколько способов создания векторных изображений в Microsoft Word.
1. Использование инструментов рисования
Microsoft Word предоставляет набор инструментов рисования, которые позволяют создавать простые фигуры и линии. Чтобы воспользоваться этими инструментами:
- Откройте документ в Microsoft Word.
- Выберите вкладку «Вставка» в верхней панели меню.
- В разделе «Иллюстрации» выберите «Фигура».
- Выберите нужную форму из выпадающего списка инструментов.
- Нажмите и удерживайте левую кнопку мыши, чтобы создать фигуру или линию на странице.
- Отпустите кнопку мыши, чтобы завершить создание фигуры или линии.
2. Импорт векторного изображения
Если у вас уже есть готовое векторное изображение в файле, вы можете импортировать его в Microsoft Word. Для этого выполните следующие действия:
- Откройте документ в Microsoft Word.
- Выберите вкладку «Вставка» в верхней панели меню.
- В разделе «Иллюстрации» выберите «Изображение».
- Выберите файл с векторным изображением на вашем компьютере и нажмите кнопку «Вставить».
3. Конвертация растрового изображения в векторный формат
Microsoft Word также предоставляет возможность конвертировать растровое изображение в векторный формат. Для этого вам понадобится дополнительное программное обеспечение, способное выполнить данную операцию. Одним из таких программных решений является Adobe Illustrator. Как пример:
- Откройте документ в Microsoft Word.
- Выберите вкладку «Вставка» в верхней панели меню.
- В разделе «Иллюстрации» выберите «Объект» и выберите «Create from File».
- Выберите растровое изображение на вашем компьютере и нажмите кнопку «Вставить».
- Следуйте инструкциям по конвертации изображения в векторный формат, используя программное обеспечение, которое вы выбрали.
- Вставьте векторное изображение в документ Microsoft Word.
Теперь вы знаете несколько способов создания векторных изображений в Microsoft Word. Вы можете использовать инструменты рисования, импортировать готовые векторные изображения или конвертировать растровые изображения в векторный формат с помощью дополнительного программного обеспечения. Пользуйтесь этими методами для создания качественных векторных изображений в Microsoft Word.

Использование математических символов
Математические символы являются неотъемлемой частью математической нотации и используются для обозначения различных математических объектов, операций и отношений. Правильное использование математических символов помогает упростить и уточнить математические выражения и формулы.
Основные категории математических символов:
- Алфавитные символы: используются для обозначения переменных и неизвестных величин в математических выражениях. Примерами таких символов являются x, y, z.
- Арифметические символы: используются для обозначения основных арифметических операций, таких как сложение (+), вычитание (–), умножение (×) и деление (÷).
- Символы отношений: используются для обозначения отношений между математическими объектами. Примеры таких символов включают знаки равенства (=), больше (>) и меньше (<).
- Символы функций: используются для обозначения математических функций, таких как синус (sin), косинус (cos) и тангенс (tan).
- Символы греческого алфавита: используются для обозначения констант, параметров и математических объектов. Примерами таких символов являются α (альфа), β (бета) и γ (гамма).
Для использования математических символов в текстовых документах, таких как Microsoft Word, можно воспользоваться различными методами:
- Использование символов из панели символов: Многие текстовые редакторы, включая Microsoft Word, предлагают встроенную панель символов, где можно выбирать и вставлять нужные математические символы.
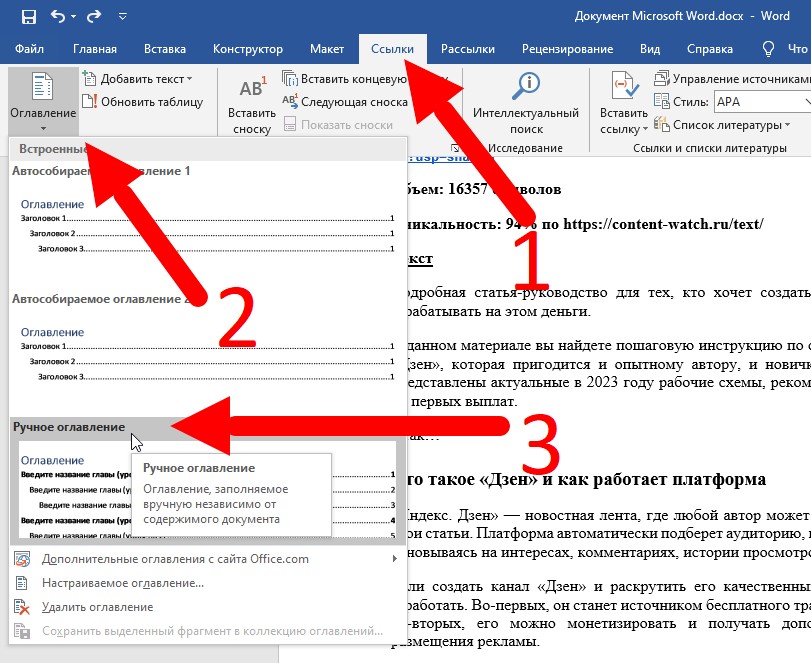
- Использование команды вставки: В Microsoft Word можно вставить математические символы с помощью команды «Вставка» → «Символы» → «Дополнительные символы». В открывшемся окне можно выбрать нужный символ и вставить его в документ.
- Использование LaTeX: LaTeX — это язык разметки, широко используемый для типографии математических формул. В LaTeX можно использовать специальные команды для вставки математических символов и формул. Затем документ LaTeX можно сконвертировать в формат Word.
Правильное использование математических символов поможет создавать четкие и понятные математические выражения и формулы. Ознакомление с основными символами и методами их использования поможет вам легко и точно передавать математические идеи и вычисления в ваших документах.

Использование символов Unicode
Символы Unicode представляют собой международный стандарт кодирования, который позволяет использовать символы любых письменностей мира, а также математические, технические и специальные символы. Они используются в различных сферах, включая печать, веб-разработку и создание документов в программе Microsoft Word.
В Word можно использовать символы Unicode, чтобы добавить необычные символы, например стрелки, музыкальные ноты или математические символы, в свои документы. Для этого можно воспользоваться следующими методами:
1. Вставка символа с помощью диалогового окна «Символы»
В Word есть встроенный диалоговый окно «Символы», которое позволяет вставлять символы Unicode в документы. Чтобы открыть это окно, нужно выбрать вкладку «Вставка» в верхней панели и нажать кнопку «Символ» в группе «Символы». В открывшемся окне можно выбрать нужный символ и нажать кнопку «Вставить», чтобы добавить его в документ.
2. Использование кодов символов Unicode
Каждый символ Unicode имеет свой уникальный код, которым можно воспользоваться для вставки символа в Word. Для этого нужно знать код символа и набрать его с помощью клавиатуры, используя нотацию hexadecimal. Например, чтобы вставить символ музыкальной ноты фа мажор, кодировка 266F, нужно ввести «266F» и нажать клавишу «Alt» и «X». Word автоматически заменит код на соответствующий символ.
3. Использование горячих клавиш для символов Unicode
Word также предоставляет возможность использовать горячие клавиши для вставки символов Unicode. Например, для вставки символа копирайта (©), можно нажать «Ctrl» + «Alt» + «C». Списки доступных горячих клавиш можно найти в интернете или изучить в документации Word.
Использование символов Unicode позволяет создавать более разнообразные и выразительные документы в Word. Комбинируя различные символы, можно создать уникальные элементы оформления, которые помогут выделиться на фоне других документов.

Форматирование вектора в Microsoft Word
Microsoft Word предоставляет различные возможности для форматирования и использования векторных изображений. Векторное изображение состоит из геометрических форм, определяемых точками, линиями и кривыми. В отличие от растровых изображений, векторное изображение можно масштабировать без потери качества.
Вставка векторного изображения
Для вставки векторного изображения в Microsoft Word следуйте следующим шагам:
- Откройте документ в Word, в который вы хотите вставить векторное изображение.
- Выберите вкладку «Вставка» в верхнем меню.
- На вкладке «Вставка» найдите группу «Изображение» и выберите опцию «Векторное изображение».
- Выберите файл с векторным изображением на вашем компьютере и нажмите «Вставить».
Редактирование и форматирование векторного изображения
После вставки векторного изображения вы можете редактировать и форматировать его в Microsoft Word. Некоторые возможности редактирования включают:
- Поворот и изменение размера изображения.
- Изменение цвета и толщины линий.
- Добавление и удаление элементов изображения.
Чтобы открыть меню форматирования векторного изображения, выделите его и нажмите правую кнопку мыши. В контекстном меню выберите «Форматировать изображение».
Сохранение векторного изображения
Когда вы закончили редактирование и форматирование векторного изображения, вы можете сохранить его в различных форматах файлов в Microsoft Word. Некоторые популярные форматы файлов включают:
| Формат файла | Описание |
|---|---|
| .docx | Формат файла Word, который сохраняет изображение и текст. |
| Популярный формат файла, который сохраняет изображение и форматирование без необходимости установки специального программного обеспечения для чтения. | |
| .svg | Формат файла Scalable Vector Graphics, который поддерживает векторное изображение и может быть открыт в различных программах. |
Для сохранения векторного изображения в одном из этих форматов выберите вкладку «Файл» в верхнем меню, выберите «Сохранить как» и выберите нужный формат файла.
Теперь, когда вы знаете, как форматировать и использовать векторные изображения в Microsoft Word, вы можете создавать профессионально выглядящие документы с векторной графикой.
Рисуем в Word векторное изображение рисованная кривая закат
Изменение размеров вектора
Изменение размеров вектора — одна из основных операций при работе с векторами. Это позволяет увеличивать или уменьшать количество элементов вектора, а также изменять их значения. В этой статье мы рассмотрим различные способы изменения размеров вектора.
Добавление элементов
Для добавления элементов в вектор существует несколько методов:
- Метод push_back: данный метод добавляет элемент в конец вектора. Новый элемент будет иметь индекс, на единицу больше, чем последний элемент вектора.
- Метод insert: этот метод позволяет добавить элемент в указанную позицию вектора. Это может быть полезно, если вы хотите вставить элемент в середину или начало вектора.
Удаление элементов
Для удаления элементов из вектора также существуют различные методы:
- Метод pop_back: данный метод удаляет последний элемент из вектора.
- Метод erase: этот метод удаляет элементы в указанном диапазоне или по указанному индексу. Он может быть полезен, если вы хотите удалить несколько элементов или определенный элемент вектора.
Изменение размера вектора
Существуют методы, которые позволяют изменять размер вектора:
- Метод resize: данный метод изменяет размер вектора заданной длины. Если новый размер больше текущего, то добавляются новые элементы, инициализированные значениями по умолчанию. Если новый размер меньше текущего, то лишние элементы удаляются. Этот метод также позволяет указать значение, которым инициализировать новые элементы.
- Метод reserve: данный метод устанавливает емкость вектора на заданное количество элементов. Это может быть полезно, если вы заранее знаете приблизительное количество элементов, которые будут в векторе, и хотите избежать повторных выделений памяти.
Изменение размеров вектора — важная операция при работе с векторами. Знание различных методов, позволяющих изменять размер вектора, является необходимым для эффективной работы с векторами в программировании.