Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
![Запуск мастера функции в Microsoft Excel]()
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
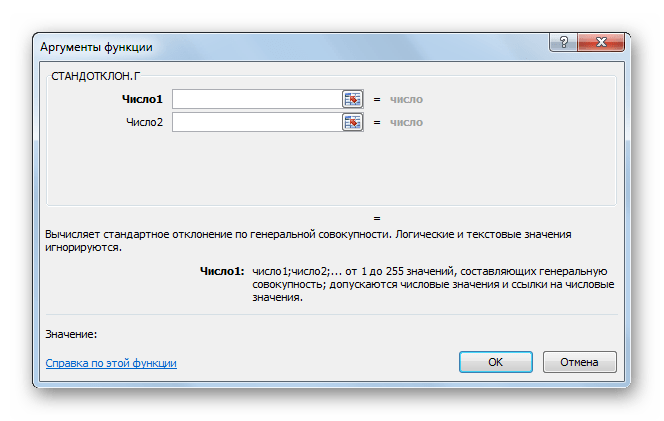
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
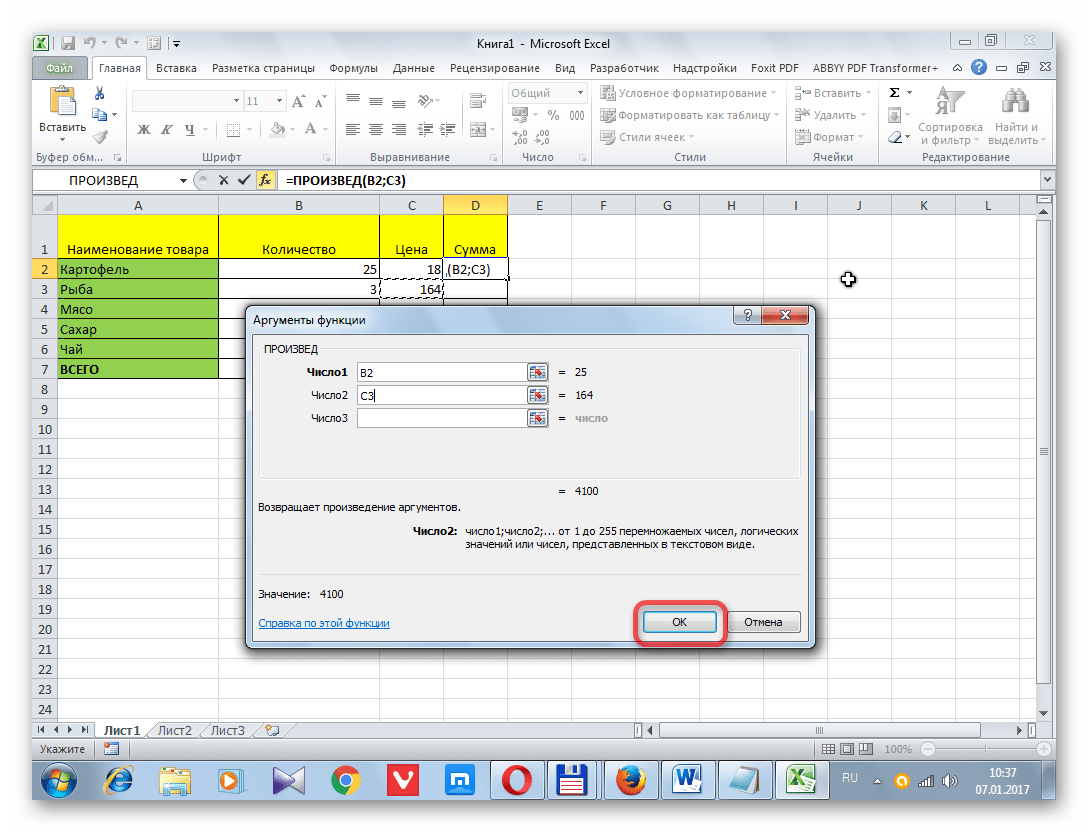
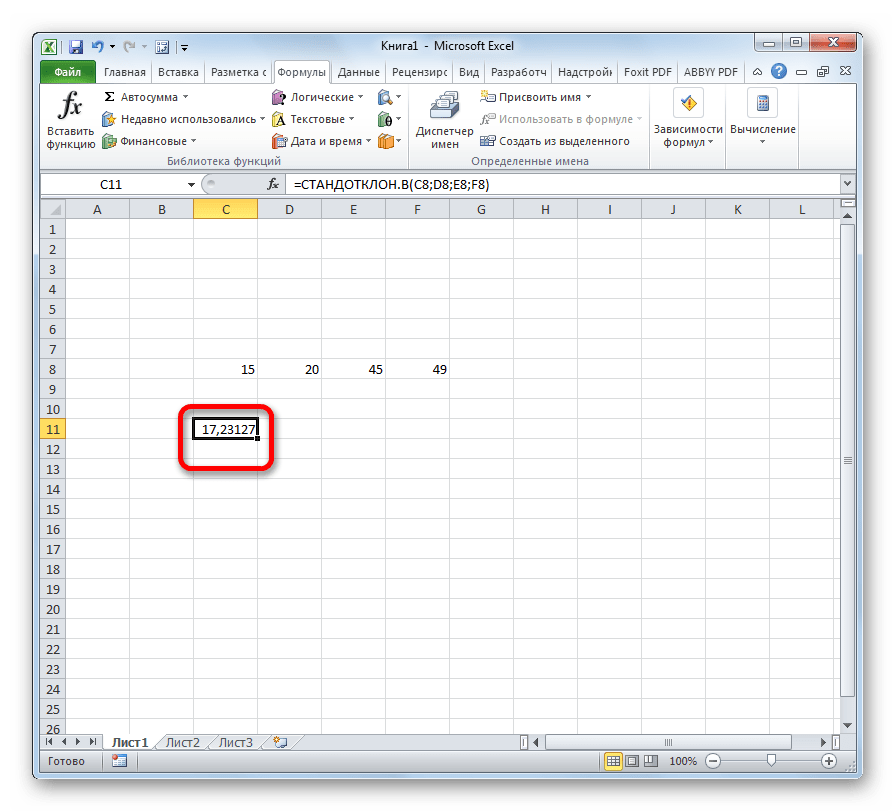
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
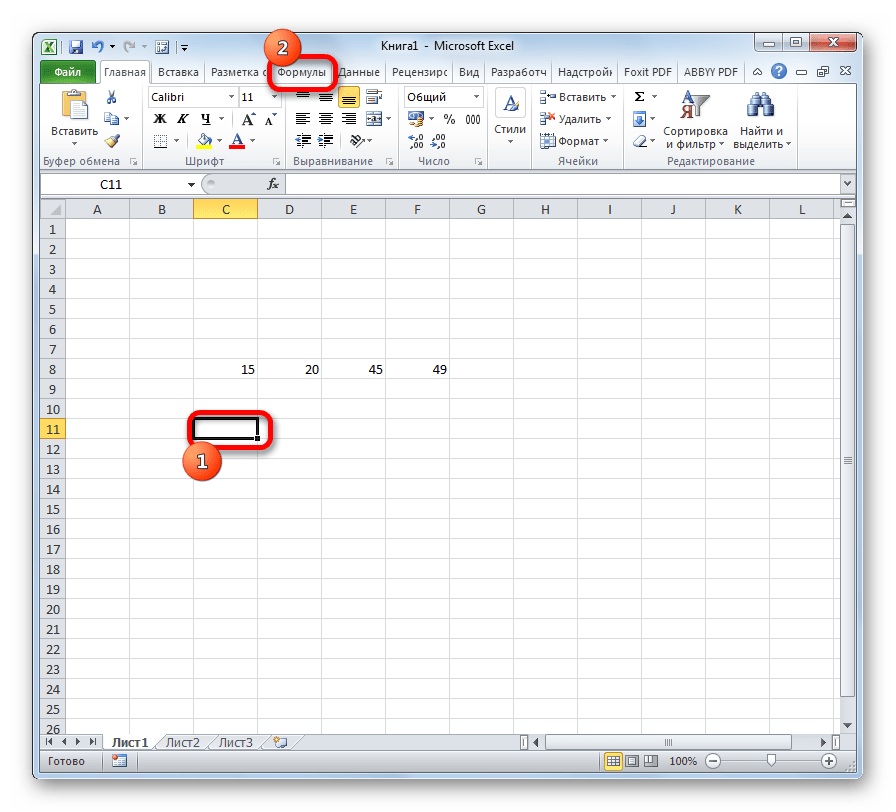
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
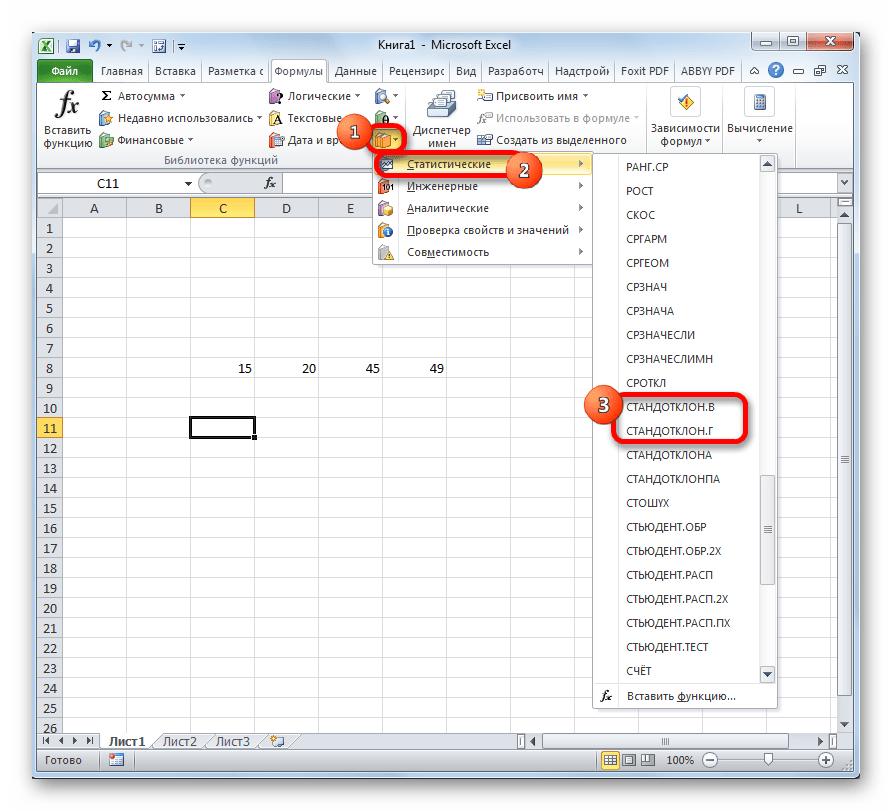
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону: =СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) или =СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…). Всего можно записать при необходимости до 255 аргументов.
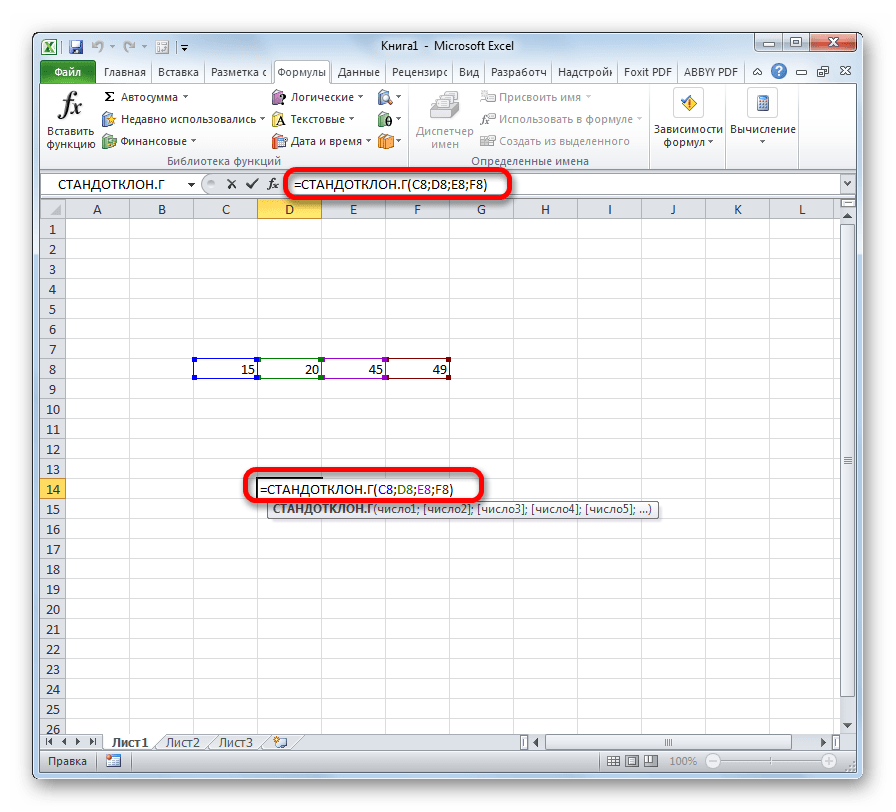
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
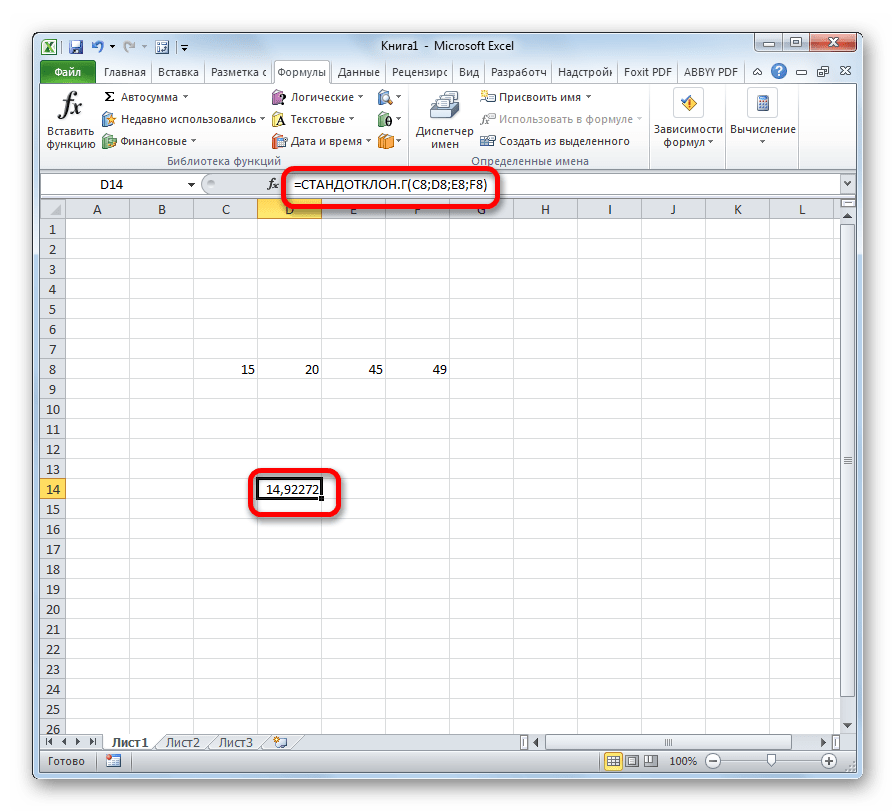
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Статистические символы
Таблица и определения символов вероятности и статистики.
Таблица вероятностных и статистических символов
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| P ( А ) | функция вероятности | вероятность события A | P ( A ) = 0,5 |
| P ( A ∩ B ) | вероятность пересечения событий | вероятность того, что событий A и B | P ( A ∩ B ) = 0,5 |
| P ( A ∪ B ) | вероятность объединения событий | вероятность того, что событий A или B | P ( A ∪ B ) = 0,5 |
| P ( A | B ) | функция условной вероятности | вероятность события A данное событие B произошло | P ( A | B ) = 0,3 |
| f ( x ) | функция плотности вероятности (pdf) | P ( a ≤ x ≤ b ) = ∫ f ( x ) dx | |
| F ( х ) | кумулятивная функция распределения (cdf) | F ( х ) = Р ( Х ≤ х ) | |
| μ | Средняя численность населения | среднее значение совокупности | μ = 10 |
| E ( X ) | ожидаемое значение | ожидаемое значение случайной величины X | E ( X ) = 10 |
| E ( X | Y ) | условное ожидание | ожидаемое значение случайной величины X с учетом Y | E ( X | Y = 2 ) = 5 |
| var ( X ) | отклонение | дисперсия случайной величины X | var ( X ) = 4 |
| σ 2 | отклонение | дисперсия значений совокупности | σ 2 = 4 |
| std ( X ) | стандартное отклонение | стандартное отклонение случайной величины X | std ( X ) = 2 |
| σ X | стандартное отклонение | значение стандартного отклонения случайной величины X | σ X = 2 |
| медиана | среднее значение случайной величины x | ||
| cov ( X , Y ) | ковариация | ковариация случайных величин X и Y | cov ( X, Y ) = 4 |
| корр ( X , Y ) | корреляция | корреляция случайных величин X и Y | корр ( X, Y ) = 0,6 |
| ρ X , Y | корреляция | корреляция случайных величин X и Y | ρ X , Y = 0,6 |
| ∑ | суммирование | суммирование — сумма всех значений в диапазоне ряда | |
| ∑∑ | двойное суммирование | двойное суммирование | |
| Пн | Режим | значение, которое чаще всего встречается в популяции | |
| MR | средний диапазон | MR = ( х макс + х мин ) / 2 | |
| Мкр | медиана выборки | половина населения ниже этого значения | |
| Q 1 | нижний / первый квартиль | 25% населения ниже этого значения | |
| 2 квартал | медиана / второй квартиль | 50% населения ниже этого значения = медиана выборки | |
| 3 квартал | верхний / третий квартиль | 75% населения ниже этого значения | |
| х | выборочное среднее | среднее / среднее арифметическое | х = (2 + 5 + 9) / 3 = 5,333 |
| с 2 | выборочная дисперсия | оценщик дисперсии выборки населения | s 2 = 4 |
| с | стандартное отклонение выборки | Оценка стандартного отклонения выборки населения | s = 2 |
| z x | стандартная оценка | z x = ( x — x ) / s x | |
| X ~ | распределение X | распределение случайной величины X | X ~ N (0,3) |
| N ( μ , σ 2 ) | нормальное распределение | гауссово распределение | X ~ N (0,3) |
| U ( а , б ) | равномерное распределение | равная вероятность в диапазоне a, b | Х ~ U (0,3) |
| ехр (λ) | экспоненциальное распределение | f ( x ) = λe — λx , x ≥0 | |
| гамма ( c , λ) | гамма-распределение | f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0 | |
| χ 2 ( к ) | распределение хи-квадрат | f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2)) | |
| F ( k 1 , k 2 ) | F распределение | ||
| Корзина ( n , p ) | биномиальное распределение | f ( k ) = n C k p k (1 -p ) nk | |
| Пуассон (λ) | распределение Пуассона | е ( К ) знак равно λ К е — λ / К ! | |
| Геом ( p ) | геометрическое распределение | f ( k ) = p (1 -p ) k | |
| HG ( N , K , n ) | гипергеометрическое распределение | ||
| Берн ( p ) | Распределение Бернулли |
Комбинаторические символы
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| п ! | факториал | п ! = 1⋅2⋅3⋅ . ⋅ n | 5! = 1⋅2⋅3⋅4⋅5 = 120 |
| n P k | перестановка | 5 п 3 = 5! / (5-3)! = 60 | |
| n C k |
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ
- Основные математические символы
- Символы алгебры
- Символы геометрии
- Статистические символы
- Логические символы
- Установить символы
- Символы исчисления
- Числовые символы
- Греческие символы
- римские цифры
БЫСТРЫЕ ТАБЛИЦЫ
Стандартное отклонение в Excel
Узнайте, как рассчитать стандартное отклонение в Microsoft Excel. Наше руководство поможет вам сделать это быстро и точно.
Как вычислить среднее квадратическое отклонение в Excel
Это мера вариации. В теории вероятностей этот показатель рассчитывается по формуле:
Путь к окну «Мастер функций» в Microsoft Office Excel. Подробный алгоритм действий на скриншоте
В Excel пользователю не нужно вручную рассчитывать стандартное отклонение. Есть несколько способов как можно быстрее найти это значение с помощью встроенных инструментов Excel. Ниже мы рассмотрим самые распространенные.
Способ 1. С помощью Мастера функций
Этот метод расчета стандартного отклонения в Excel занимает минимальное время. Расчет производится следующим образом:
- С помощью левой клавиши манипулятора на рабочем листе программы выберите ячейку, в которой будет отображаться результат расчета.
- Нажмите кнопку «Вставить функцию», расположенную слева от строки ввода.

- После завершения предыдущего шага откроется окно мастера. Здесь пользователю нужно будет найти строку «STDEV.V», выбрать ее с помощью ЛКМ и нажать «ОК» в нижней части меню. Список функций также содержит записи «STDEV.G» и просто «STDEV». На них не нужно нажимать!
- Выберите нужную функцию для расчета стандартного отклонения в Excel
- В следующем окне аргументов функции вам нужно записать численность населения в каждом поле. Если эти значения уже записаны на листе Excel, вы можете указать координаты соответствующих ячеек.
- Когда все строки будут заполнены, нажмите «ОК» в нижней части меню «Аргументы функций.
- Завершение окна «Аргументы функции». Здесь нужно указать координаты ячеек из массива таблицы с соответствующими числовыми значениями
- Проверить результат. На первом шаге в выделенной ячейке будет записано число. Это стандартное отклонение.
- Окончательный результат. Значение стандартного отклонения отображается в выделенной ячейке
Примечание! Если после выполнения описанных выше манипуляций в ячейке появятся символы «###», то результат — большое число и ячейку нужно растянуть.
Способ 2. Расчет стандартного отклонения в разделе «Формулы»
вы также можете рассчитать стандартное отклонение на вкладке «Формулы» в Excel. Алгоритм расчета состоит из следующих шагов:
- Используя аналогичный шаблон, выберите любые свободные ячейки на листе. В дальнейшем результат будет отображаться в этом элементе.
- Найдите слово «Формулы» в столбце инструментов в верхней части главного меню программы и щелкните по нему ЛКМ.
- Перейти в раздел формул в Excel
- В открывшейся области найдите подраздел «Библиотека функций», затем разверните вкладку «Дополнительные функции».
- В контекстном меню выберите тип «Статистика» и наведите курсор мыши на это слово.
- Появится дополнительное контекстное окно, в котором пользователь должен щелкнуть строку «STDEV.V».

Шаги по выбору формулы стандартного отклонения
- В открывшемся окне «Аргументы функции» необходимо заполнить два поля, указав координаты соответствующих ячеек на листе или в массиве таблицы. Требуемые значения также можно ввести вручную.
- После выполнения этих манипуляций нажмите «ОК».
- Заполнение полей в меню «Аргументы функции»
- Убедитесь, что результат формулы отображается в ячейке, указанной выше, числом, характеризующим стандартное отклонение.
Важно! Если необходимо рассчитать стандартное отклонение нескольких параметров, исходную формулу можно распространить на остальные ячейки матрицы таблицы.
Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
Для расчета стандартного отклонения в Microsoft Office Excel можно ввести специальную формулу с клавиатуры, результат будет таким же. Этот метод расчета состоит из выполнения следующих шагов:
- Поместите курсор мыши в ячейку, где будет отображаться результат.
- В выделенном элементе введите с клавиатуры формулу «= СТАНДОТКЛОН (a, b, c, d)». Вместо букв в скобках нужно указать соответствующие аргументы. Это числа из массива табличных данных.

Пример написания формулы для расчета стандартного отклонения в Excel
- Нажмите «Enter», чтобы завершить процедуру.
- Проверить результат. В результате в ячейке должно отображаться определенное значение стандартного отклонения.
- Окончательные результаты
Дополнительная информация! Формула «STANOTELON.G ()» также может использоваться для расчета. Результат будет идентичным. Этот метод будет работать независимо от версии программного обеспечения.
Способ 4. Ручной подсчет
Это нецелесообразно в Microsoft Office Excel. Этот метод основан на использовании обычного калькулятора, также присутствующего в Excel. Для ручного подсчета необходимо выполнить следующие действия по алгоритму:
- Используя левую клавишу манипулятора, выберите ячейку массива таблицы, в которую будет выводиться результат.
- Поставьте знак «=» и с клавиатуры компьютера введите числовые значения для расчета стандартного отклонения, указав координаты соответствующих ячеек с планшета. Здесь нужно подставить параметры в формулу из первой цифры.
- После написания формулы нажмите «Ввод» и убедитесь, что в ячейке отображается результат стандартного отклонения.
Примечание! Вы также можете растянуть формулу Excel, чтобы вычислить стандартное отклонение для оставшихся ячеек, чтобы заполнить их автоматически.
Заключение
Таким образом, стандартное отклонение в Microsoft Office Excel рассчитывается с использованием формулы или путем выбора соответствующей функции. Основные методы расчета этого параметра обсуждались выше.